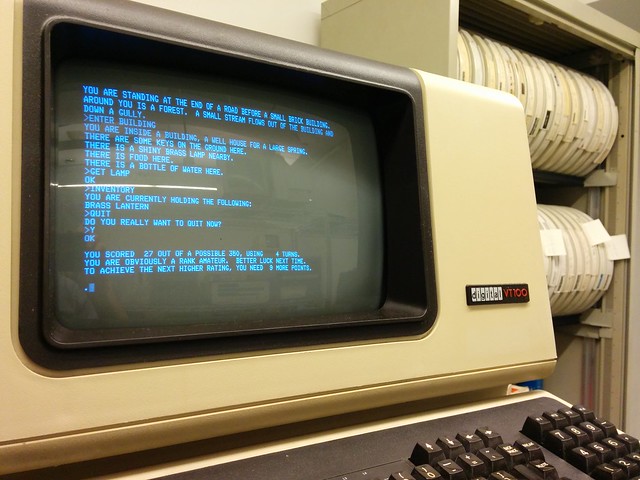
Two weeks ago we salvaged two PDP-11/34 minicomputers, VT1xx terminals and assorted parts. Since then we’ve spent some quality time in the 1970s, cleaning Unibus contacts, reseating cards and replacing bad capacitors in the VT100 analog boards. Both of the…
We rescued two PDP-11/34 computers and their associated equipment from a storage unit in the Bronx and have been working on getting them running again. The computing system included multiple RK05 hard drives, two RL02 decpack drives, a TU11 tape…
A few months ago we introduced Octoscroller, NYC Resistor’s eight-sided RGB LED matrix display built with jumbtotron RGB LED matrix panels. The interface “cape” has been reworked twice and the LEDscape source code has been refined to handle various arrangements…
Did you ever notice how beat-up the floors were at NYC Resistor? Four years of rolling chairs had done horrible things to the paint, so we did something about it last night. Everybody pitched in with a massive effort. While…
The Spikenzie Labs Solder:Time Desk Clock is a fun through-hole kit to solder together. It includes a snap-together lasercut acrylic case with a really nice red tinted screen that increases the contrast on the 20×7 red LED matrix. Plus it…
Given a set of points, the Voronoi tessellation creates a set of convex polygons that each contain one point. They can also be used to randomly generate unique art pieces that cast shifting, lace-like shadows. This one was really quite…
It is a truth, universally acknowledged, that an engineer in possession of an antique computer must be in want of hacking it. Last year I reverse engineered the Easter Egg photographs from a Mac SE that I found on the…
Next weekend at NYC Resistor we are teaching a class on the Adafruit FLORA and Neopixel. These round Arduino compatible controller boards are a great base for wearable projects like watches, jackets and neck ties, as well as holiday decorations.…
Last year we wrote about building HID Proxcard RFID tags with attiny85 microcontrollers (based on Micah’s avrfid.s code). The C version only supported classic 26-bit cards, but I recently needed to support the “secure” HID Corporate 1000 35-bit format. Based…
The PUMA 260 robot arm that was hanging around NYC Resistor was seen heading into Manhattan on the subway.